Nicholas Owad
Straight knots
One of my current research topics
Download Research Statement Download Research PapersSee all the knots with 10 or less crossings
I wrote some code to let anyone draw a straight knot! There are lots of knots already programmed in to let you just browse too. To draw your own, just enter the straight code, which you can learn more about on the page. Try it out!

Submitted Work
Every knot has a straight diagram
A diagram is straight if there is a single arc, that doesn't cross itself, and contains all the crossings. Every knot has a straight diagram and therefore, we can make an invariant, called the straight number. Usually, one must increase the number of crossings in a diagram to make it straight. How many new crossings do we need? Is this invariant related to other invariants? Please look at the paper Straight knots to find the answers to these questions and more.
How many new crossings do we need?
In the first paper, we introduced straight number. Now we want to find the interesting properties of the invariant. It seems hard to prove a family of knots has straight number strictly larger than crossing number. We found the first infinite family of knots which has this property and produce a method for generating other families of knots that are not perfectly straight. For all the details, please look at the paper Families of not perfectly straight knots.
Future Work
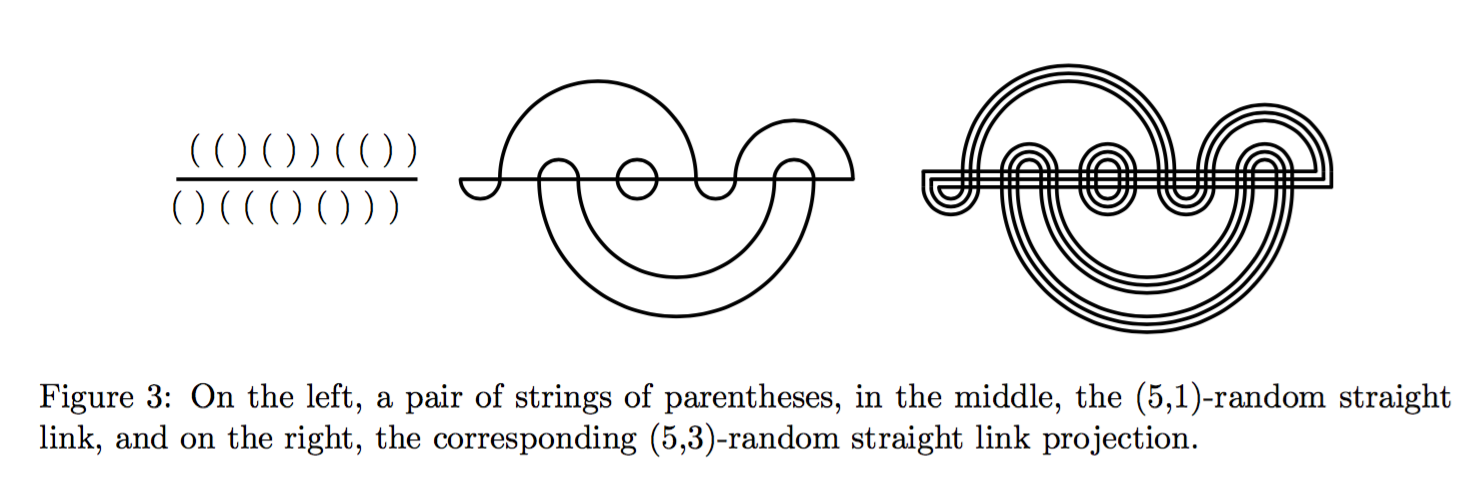
Random Straight links
with Anastasiia Tsvietkova
Thanks to recent work by Even-Zohar, Hass, Linial, and Nowik, we have produced a random link model called random straight links. Then we use the remarkable results Lackenby, Agol and Thurston to get bounds on the expectation of the volume of these links.
Snail links and volume
with Jessica Purcell
There is some strong numerical evidence that straight number is related to volume. How exactly is unclear. But here are two visualizations of the same data set that I have made that are really exciting. They shows the first 249,500 snail links, which is a class of link I defined in my work. Each frame of the video is a slice of the image above it, moving from back to front. Look for the paper in the coming months!